if n balls are distributed randomly into n boxes I was thinking that if we have $n$ balls and $n-1$ bins to distrubute this balls then . $79.00
0 · probability of n ball distribution
1 · n n balls probability
2 · n box probability
3 · n balls randomly placed
4 · n balls in n boxes
5 · n balls empty box probability
6 · how to distribute n boxes
7 · distribution of balls into boxes pdf
This convertible under-cabinet hood, designed to work with smaller cooking .
Each of n balls is independently placed into one of n boxes, with all boxes equally likely. What is the probability that exactly one box is empty? (Introduction to Probability, Blitzstein and Nwang, p.36). The number of possible permutations with replacement is nn. In order to have one .I was thinking that if we have $n$ balls and $n-1$ bins to distrubute this balls then .
Randomly select a box from $ boxes, where $ balls are randomly .We have n distinguishable balls (say they have different labels or colours). If these .Question: Randomly distribute r balls in n boxes. Find the probability that the first . I was thinking that if we have $n$ balls and $n-1$ bins to distrubute this balls then by the multiplicative principle we have $n^{n-1}$ ways to do that. however instead, you are .
probability of n ball distribution
Randomly select a box from $ boxes, where $ balls are randomly distributed. Is the geometric distribution a suitable approach? $P(n) =p^nq$In this case, we have k identical balls, to be distributed into n distinguishable boxes, but with no restriction on the number of balls that can occupy a given box. As in the last case, since the .The M M balls are randomly distributed into the N N boxes. What is the expected number of empty boxes? I came up with this formula: ∑N i=0 i(N i)(N−i N)M ∑ i = 0 N i (N i) (N − i N) M. .
Suppose that n distinct balls are randomly distributed into N boxes, where all Nn arrangements are equally likely. Find the probability that exactly m balls fall into the first box, where m ≤ n.Suppose n balls are randomly distributed into n boxes. (a) What is the probability that no box is empty? (b) What is the probability that exactly one box is empty? (c) What is the probability . We have n distinguishable balls (say they have different labels or colours). If these balls are dropped at random in n boxes, what is the probability that: 1- No box is empty? 2- .Question: Randomly distribute r balls in n boxes. Find the probability that the first box is empty. I think I should make the question into 3 cases, namely, r=n, rn. CASE r=n: ${r .
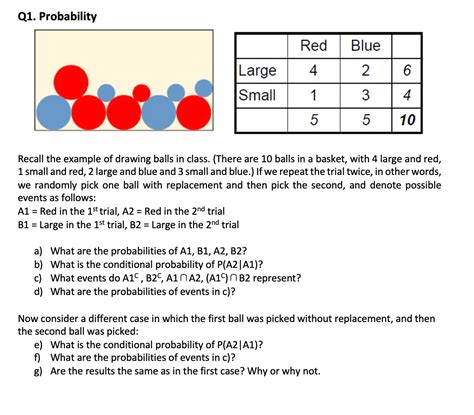
If n distinct objects are distributed randomly into n distinct boxes, what is the probability that (a) No box is empty? (b) Exactly one box is empty? (c) Exactly two boxes are empty? ( PART A ) Each desirable outcome is a surjection from an n set to a n-1 set. The total number of outcomes is the number of functions from an n set to an n-1 set.Counting problems have always intrigued me, and I'm working on some out of interest. The other thread on this topic had unsatisfactory answers, because they don't match the answer in my book. My
There are n balls labeled 1 through n, and n boxes labeled 1 through n. The balls are distributed randomly into the boxes, one in each box, so that all n! permutations are equally likely. Say that a match occurs at place i if the ball labeled i happens to fall in the box labeled i. Let M be the total number of matches. a) Find E(M). b) Find SD(M).Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
Suppose N balls are distributed at random into r boxes, where N is Poisson distributed with mean λ \lambda λ. Let Y denote the number of empty boxes. Show that Y is binomially distributed with parameters r and p = e − λ / r p=e^{-\lambda / r} p = e − λ / r.
$\begingroup$ Notice I'm not asserting distinguishable balls, merely that each ball has a cell. We are always free to order the balls, as long as we remember to disregard our artificial ordering by the time we are finished. (This is analogous to the freedom to pick any basis you like in linear algebra to compute something. Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteSuppose n balls are distributed at random into r boxes. Find the probability that there are exactly k balls in the first r1 boxes (here r1 < r). Here’s the best way to solve it.
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteSuppose n balls are distributed into n boxes so that all the n^n possible arrangements are equally likely. Compute the probability that only 1 is empty. Added by Kevin B. Instant Answer. Step 1. There are n ways to do this. Show more. Show all steps. View the full answer . $\begingroup$ In the linked problem, the first ball can go into the first box. The second ball can go into the first or the second box. The third can go into the first, second, or third box, and so on. $\endgroup$ – If n distinct balls are distributed at random into N (N> n) boxes, what is the probability that no box will receive more than one ball (each box will receive at most one ball)? 00:57 Five distinct balls are randomly placed in three boxes, labeled A, B, and C, so that each ball is equally likely to be in each of the boxes, independently of other .
(1) [35 marks] Suppose n balls are thrown randomly into m boxes. Each ball lands in each box with uniform probability. Define Xi be the r.v. equal to the number of balls that land in box i. - What is the distribution of Xi ? Compute E[Xi] and Var[Xi]. [15 marks] - Are the Xi r.v's (i) mutually independent (ii) pairwise independent?Suppose that n balls are distributed into n boxes so that all of the na possible arrangements are equally likely. We would like to compute the probability that only box 1 is empty. Let A be the event that only box 1 is empty. Let B; be the event that box j, j = 2, ., n, has two balls, box 1 has no balls, and remaining (n - 2) boxes have . Problem: If $n$ balls are distributed at random into $r$ boxes (where $r \geq 3$), what is the probability that box $ at exactly $j$ balls for I'm going to answer the problem based on my interpretation(s). I try to state them as clearly as possible. I'm only dealing with part a) of the problem. \leq j \leq n$ and .Suppose 10 balls, numbered 1-10, are to be distributed randomly into 10 boxes. a. What is the probability all 10 balls are placed into one box? b. What is the probability that no boxes are empty? We put k balls into n boxes at random. What is the probability that no box remains empty?
Question: Questions: 1. If n distinct balls are distributed at random into N(N>n) boxes, what is the probability that no box will receive more than one ball (each box will receive at most one ball)? 2. 8 people including Mr. T and Mr. K are arranged in a linear order.4) The number of ways to distribute k indistinguishable balls into n distinguishable boxes, without exclusion, in such a way that no box is empty, is k 1 n 1 Here is a summary of our results: Theorem # Balls Boxes Excl No box empty # ways of putting k balls into n boxes 1 Dist Dist with n k n n 1 n 2 n k 1 5 -1 Dist Dist with yes n! if k n 0 if .
You run into a problem here. As I commented, (and as a subsequent answer has explained in detail), the formula you write is valid only for distinguishable balls in distinguishable boxes.. Further, if the balls are treated as indistinguishable, the unrestricted number of ways can be found out by stars and bars as $\binom{n+m-1}{n} = D\;\;(say)$ ways, but these are not .You have $N$ boxes and $M$ balls. The $M$ balls are randomly distributed into the $N$ boxes. What is the expected number of empty boxes? I came up with this formula:
n n balls probability
Question: 5. Suppose n balls are randomly distributed into n boxes. (a) What is the probability that no box is empty? (b) What is the probability that exactly one box is empty? (c) What is the probability that at least one box is empty? Depending on how you mean the balls are "randomly distributed", your answer could be correct or incorrect. If by "randomly distributed" you mean that each way to distribute the indistinguishable balls is equally likely (i.e. the "stars and bars" distribution $***|*|*|*$ has equal probability to $*|*|**|**$), then your answer is perfect.. If by "randomly distributed" you mean .
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
1. m balls are randomly distributed into n boxes. What is the probability that the first box is empty? What is the expected number of balls in the first box? 2. A security team has a bunch of n similar keys, only one of which fits a lock. They decide to try keys at random until the correct one is .
Suppose n balls are distributed at random into r boxes. Let X i = 1 X_{i}=1 X i = 1 if box i is empty and let X i = 0 X_{i}=0 X i = 0 otherwise. (a) Compute E X i E X_{i} E X i . (b) For i ≠ j, i \neq j, i = j, compute E (X i X j) E\left(X_{i} X_{j}\right) E (X i X j ). (c) Let S r S_{r} S r denote the number of empty boxes. Write As recommended by @pbuk in the post #14, the problem of putting n indistinguishable balls into m distinguishable boxes, where ## n\ge m ## and ## m\gt 0 ## can be solved by using “stars and bars” method. The total number of outcomes $$ \binom{n+m-1}{n} $$ The number of outcomes when only the first k boxes are left empty and where ## 0\le k .
n box probability
n balls randomly placed
who makes steel glide tool boxes
Metal Supermarkets offers a variety of shapes and grades of bronze, cut to the size you need, including: 932 and 954. Select from one of the available shapes below to get started. Or contact your closest store for assistance with metal sourcing.
if n balls are distributed randomly into n boxes|n box probability